MATHEMATICS

FIRST TERM 

WEEK 4

PRIMARY 5

THEME – NUMBER AND NUMERATION

PREVIOUS LESSON – 

TOPIC: FRACTION, DECIMAL AND PERCENTAGES

LEARNING AREA 

1. Introductory Activities

2. Meaning and Types of Fractions

3. Relationship between Improper and Mixed Fractions

4. Meaning of Decimal Fractions

5. Relationship between Decimals and Fractions

6. Meaning of Percentages

7. Relationship between Percentages, Decimals and Fractions

8. Lesson Evaluation and Weekly Assessment (Test)

 

PERFORMANCE OBJECTIVES

By the end of the lesson, most of the pupils should have attained the following objectives –

1. change fraction to decimals and decimals to percentages and vice versa.

2. solve quantitative aptitude problems related to percentages.

3. state the relationship between fraction and ratio.

4. solve quantitative aptitude problems related to ratio.

ENTRY BEHAVIOR

The pupils can identify and describe decimal fractions.

 

INSTRUCTIONAL MATERIALS

The teacher will teach the lesson with the aid of –

1. Fraction-Decimal conversion chart.

2. Fraction-Percentage chart.

3. Decimal-Percentage conversion chart.

4. Percentage-Decimal conversion chart.

5. Fla sh card.

METHOD OF TEACHING 

Choose a suitable and appropriate methods for the lessons.

Note – Irrespective of choosing methods of teaching, always introduce an activities that will arouse pupil’s interest or lead them to the lessons. 

REFERENCE MATERIALS

Scheme of Week

9 – Years Basic Education Curriculum

Fundamentals of Cultural and Creative Art for Basic 6

All Relevant Materials

Online Information

 

CONTENT OF THE LESSON

LESSON 1 – INTRODUCTION TO FRACTIONS

ACTIVITY 1

Fractions are numbers that represent a part of the whole.

A fraction is a number that has two parts, a whole number and a fraction.

When an object or a group of objects is divided into equal parts, then each individual part is a fraction.

A fraction is usually written as 1/2 or 5/12 or 7/18 and so on.

It is divided into a numerator and denominator where the denominator represents the total number of equal parts into which the whole is divided.

The numerator is the number of equal parts that are taken out.

For e.g. in the fraction 3/4, 3 is the numerator and 4 is the denominator.

ACTIVITY 2 – Real LIFE EXAMPLE OF A FRACTION 

Sharing of an objects within two or more parts.

 

2/3

ACTIVITY 3 – TYPES OF FRACTIONS 

There are three (3) of fractions,

1. Proper Fraction

2. Improper Fraction

3. Mixed Fraction

In a fraction there are two simple possibilities:

• The numerator is smaller than the denominator

• The numerator is bigger than the denominator

PROPER FRACTION 

In proper fraction, the numerator is smaller than the denominator.

For example – 3/5, 7/9, etc.

 

IMPROPER FRACTION 

Improper fraction is a fraction that has the numerator is larger than the denominator.

For example – 5/3, 9/7, etc.

MIXED FRACTION

A mixed number is made up of a whole number and a fraction.

A mixed fraction is a fraction with a whole number and a fraction.

For example – 1 2/3, 5 6/11, etc.

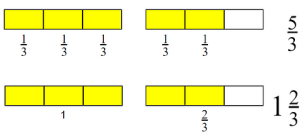
ACTIVITY 4 – IMPROPER FRACTION TO MIXED FRACTIONS 

 

5/3 = 1 2/3

11/5 = 2 1/5

9/2 = 4 1/2

5/3

= (3 + 2)/3

= 1 + 2/3

= 1 2/3

11/5

= (5 + 5 + 1)/5

= 1 + 1 + 1/5

= 2 + 1/5

= 2 1/5

9/2

= (2 + 2 + 2 + 2 + 1/2)

= 1 + 1 + 1 + 1 + 1/2

= 4 + 1/2

= 4 1/2

 

ACTIVITY 5 – MIXED FRACTION TO IMPROPER FRACTIONS  

1 2/3

= (1 x 3 + 2)/3

= (3 + 2)/3

= 5/3

2 1/5

= (2 x 5 + 1)/5

= (10 + 1)/5

= 11/5

 

4 1/2

= (4 x 2 + 1)/2

= (8 + 1)/2

= 9/2

LESSON EVALUATION 

Convert to mixed fractions –

1. 46/3

2. 49/5

3. 63/8

Convert to Improper fractions –

4. 15 1/3

5. 12 1/4

6. 16 2/5

LESSON 2 – DECIMAL FRACTIONS 

ACTIVITY 1 – INTRODUCTION 

A decimal fraction is a number that has two parts, a whole number and a fraction.

The two parts are separated by a point known as the decimal point, for example, 1.25.

The digits before the point represent whole numbers. The digits after the point represent fractions.

Both parts make up a decimal fraction.

ACTIVITY 2 – DECIMAL FRACTIONS TO FRACTIONS 

We can convert a decimal Fraction to its fraction.

0.1 = 1/10    0.01 = 1/100   0.001/1000

0.2 = 1/10    0.02 = 2/100   0.002/1000

0.3 = 3/10    0.03 = 3/100   0.003/1000

0.4 = 4/10    0.04 = 4/100   0.004/1000, etc.

 

Convert 0.37 to fraction.

0.37

= 0.3 + 0.07

= 3/10 + 7/100

= (30 + 7)/100

= 37/100

Convert 3.25 to fraction.

3.25

= 3 + 0.2 + 0.05

= 3 + 2/10 + 5/100

= 3 + (20 + 5)/100

= 3 + 25/100

= 3 25/(25 + 25 + 25 + 25)

= 3 25¹/(25¹ + 25¹ + 25¹ + 25¹)

= 3 1/4

ACTIVITY 3

Convert 37/100 to decimal fraction.

37/100 can be written as (30 + 7)/100

= 30/100 + 7/100

= 3/10 + 7/100

= 0.3 + 0.07

0.30

+ 0.07

_______

0.37

Therefore,

37/100 = 0.37

 

Covert 3 1/4 to decimal fraction.

3 1/4

= 3 + (1 x 25)/(4 x 25)

= 3 + 25/100 = 3 + 0.25 = 3.25

OR

= 3 + (20 + 5)/100

= 3 + 20/100 + 5/100

= 3 + 2/10 + 5/100

= 3 + 0.2 + 0.05

= 3.25

LESSON EVALUATION

Covert to fractions.

1. 0.35

2. 1.58

3. 7.32

 

Covert to decimal fractions.

1. 35/100

2. 1 27/50

3. 1 13/20

LESSON 3 – PERCENTAGES 

ACTIVITY 1 

A percentage is a number expressed as a fraction of 100.

That’s, fractions with 100 as denominators are known as Percentages.

% is a symbol for percentage.

For example,

15% = 15/100 = 0.15

23% = 23/100 = 0.23

65% = 65/100 = 0.65

ACTIVITY 2 – RELATIONSHIP BETWEEN FRACTIONS, DECIMALS AND PERCENTAGES 

1. Convert 65% to fraction and decimal.

To fraction,

65%

= 65/100

= (5¹ x 13)/(5¹ x 20)

= (1 x 13)/(1 x 20)

= 13/20

To decimal fraction,

65/100

= (60 + 5)/100

= 60/100 + 5/100

= 0.60 + 0.05

= 0.65

2. Convert 13/20 to percentage and decimal.

To percentage,

13/20

= (13 x 5)/(20 x 5) Hint – 5 = 100/20

= 65/100

To decimal fraction,

65/100

= (60 + 5)/100

= 60/100 + 5/100

= 0.60 + 0.05

= 0.65

3. Convert 0.65 to fractions and decimal.

0.65

= 6/10 + 5/100

= 60/100 + 5/100

= (60 + 5)/100

= 65/100

0.65

= 65/100 (65/100 means 65 out of 100).

Therefore,

0.65 = 65%

LESSON EVALUATION 

Copy and complete the following chart,

 

LESSON 4 – REVISION AND LESSON EVALUATION 

PRESENTATION

To deliver the lesson, the teacher adopts the following steps:

1. Revises the previous lesson based on the previous lesson or pupil’s knowledge.

2. Creates activities on sharing.

3. Uses the activities to introduce the of fraction.

4. Explains the meaning and types of of fractions.

Pupil’s Activities – Participate actively in sharing activities and the meaning and types of fractions.

5. Guides pupils to understand the relationship between improper and mixed fractions.

Pupil’s Activities – Pay attention to the relationship between improper and mixed fractions.

6. Displays chart showing the relationship between decimals and fractions.

Pupil’s Activities – Study the relationship between decimals and fractions.

7. Leads pupils to express decimals to fractions and fractions to decimals.

Pupil’s Activities – Change decimals to fractions and fractions to decimals.

8. Displays chart showing the relationship between percentages, decimals and fractions.

Pupil’s Activities – Study the chart.

9. Leads pupils to understand the relationship between percentages, decimals and fractions.

Pupil’s Activities – Express percentages to fractions and decimals, vice versa.

• Solve quantitative aptitude problems related to fractions, decimals and percentages.

CONCLUSION

To conclude the lesson for the week, the teacher revises the entire lesson and links it to the following week’s lesson.

NEXT LESSON

LESSON EVALUATION

As stated in the lesson evaluations.